Bootstrapping

October 7 + 9 + 16, 2024

Author

Jo Hardin

Agenda 10/7/24

Review: logic of SE
Logic of bootstrapping (resample from the sample with replacement)
BS SE of a statistic

Why bootstrap?

Motivation:

to estimate the variability and distribution of a statistic in repeated samples of size \(n\) (not dependent on \(H_0\) being true).

Variability

standard deviation of the data: \(s = \sqrt{\frac{\sum_{i=1}^n(X_i - \overline{X})^2}{n-1}}\)
standard error of the statistic: depends…

Intuitive understanding

See in the applets for an intuitive understanding of both confidence intervals and boostrapping:

StatKey applets which demonstrate bootstrapping.
Confidence interval logic from the Rossman & Chance applets.

Basic Notation

(n.b., we don’t ever do what is on this slide)

Let \(\theta\) be the parameter of interest, and let \(\hat{\theta}\) be the estimate of \(\theta\). If we could, we’d take many samples of size \(n\) from the population to create a sampling distribution for \(\hat{\theta}\). Consider taking \(B\) random samples from the population.

\[\begin{align} \hat{\theta}(\cdot) = \frac{1}{B} \sum_{i=1}^B \hat{\theta}_i \end{align}\] is the best guess for \(\theta\). If \(\hat{\theta}\) is very different from \(\theta\), we would call it biased. \[\begin{align} SE(\hat{\theta}) &= \bigg[ \frac{1}{B-1} \sum_{i=1}^B(\hat{\theta}_i - \hat{\theta}(\cdot))^2 \bigg]^{1/2}\\ q_1 &= [0.25 B] \ \ \ \ \hat{\theta}^{(q_1)} = \mbox{25}\% \mbox{ cutoff}\\ q_3 &= [0.75 B] \ \ \ \ \hat{\theta}^{(q_3)} = \mbox{75}\% \mbox{ cutoff}\\ \end{align}\]

Ideally

(we never do part (a))

From Hesterberg et al., Chapter 16 of Introduction to the Practice of Statistics by Moore, McCabe, and Craig

Bootstrap Procedure

Resample data with replacement from the original sample.
Calculate the statistic of interest for each resample.
Repeat 1. and 2. \(B\) times.
Use the bootstrap distribution for inference.

Bootstrap Notation

(n.b., bootstrapping is the process on this slide)

Take many ( \(B\) ) resamples of size \(n\) from the sample to create a bootstrap distribution for \(\hat{\theta}^*\) (instead of the sampling distribution for \(\hat{\theta}\)).

Let \(\hat{\theta}^*(b)\) be the calculated statistic of interest for the \(b^{th}\) bootstrap sample. The best guess for \(\theta\) is: \[\begin{align} \hat{\theta}^* = \frac{1}{B} \sum_{b=1}^B \hat{\theta}^*(b) \end{align}\] (if \(\hat{\theta}^*\) is very different from \(\hat{\theta}\), we call it biased.) And the estimated value for the standard error of the estimate is \[\begin{align} \hat{SE}^* = \bigg[ \frac{1}{B-1} \sum_{b=1}^B ( \hat{\theta}^*(b) - \hat{\theta}^*)^2 \bigg]^{1/2} \end{align}\]

What do we get?

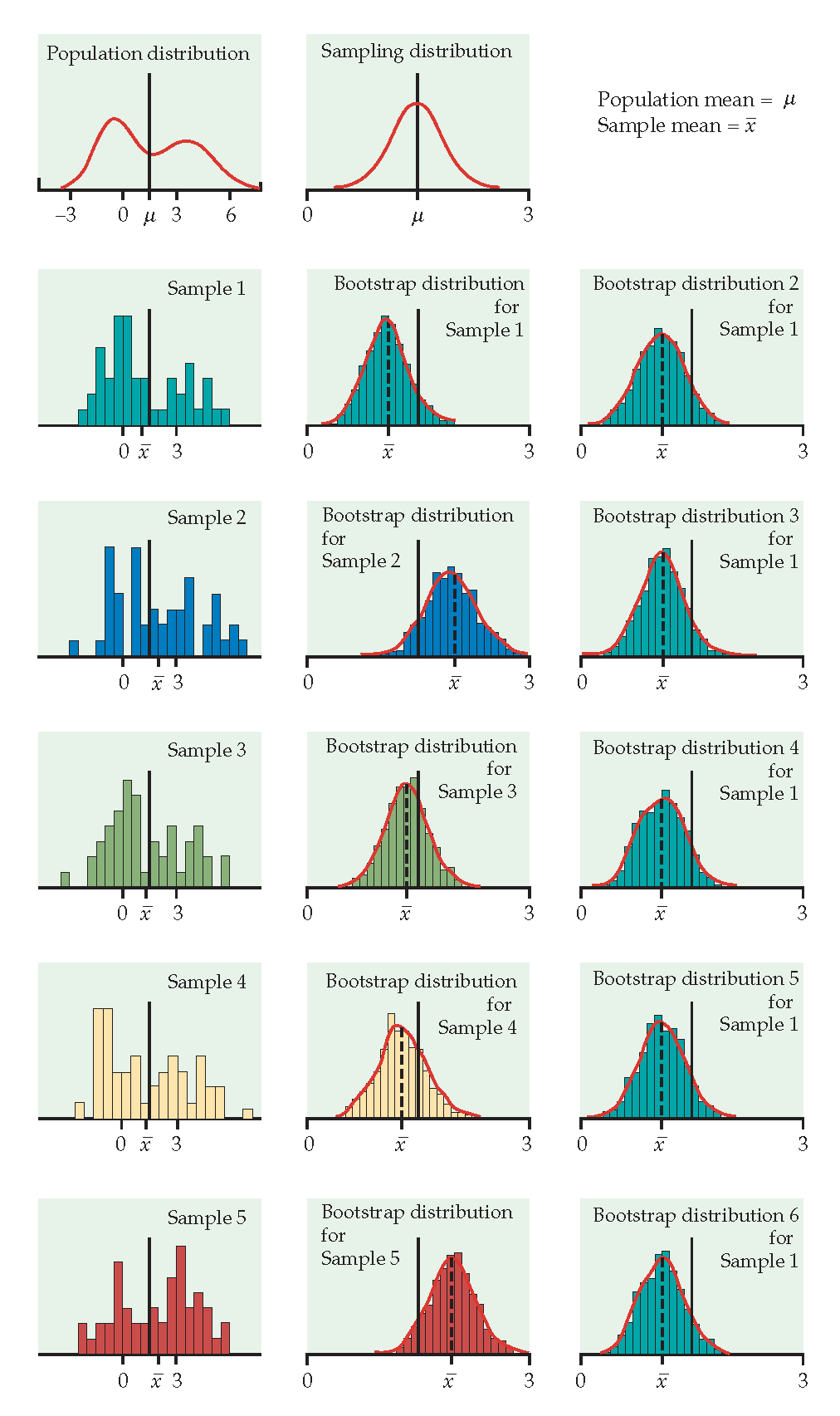
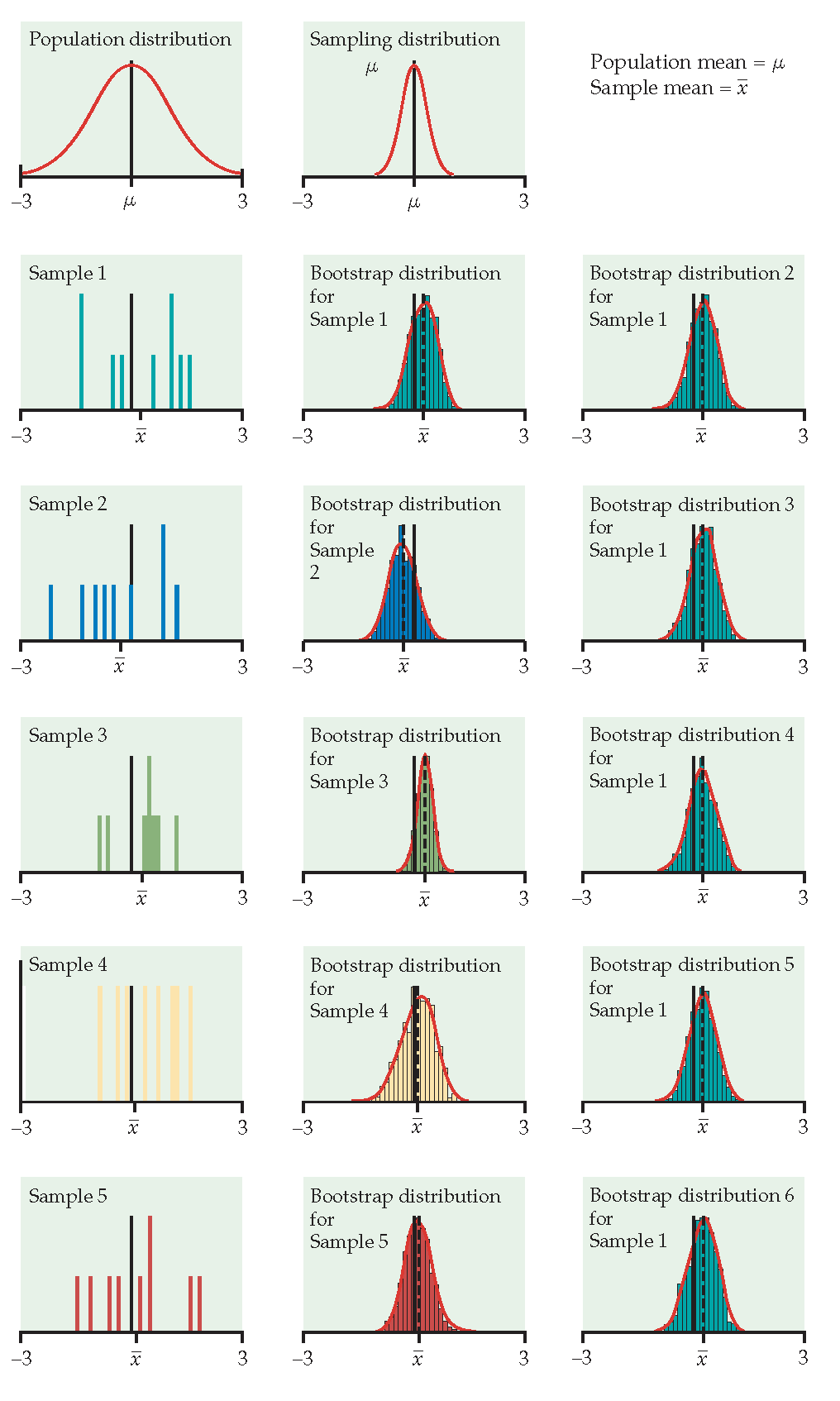
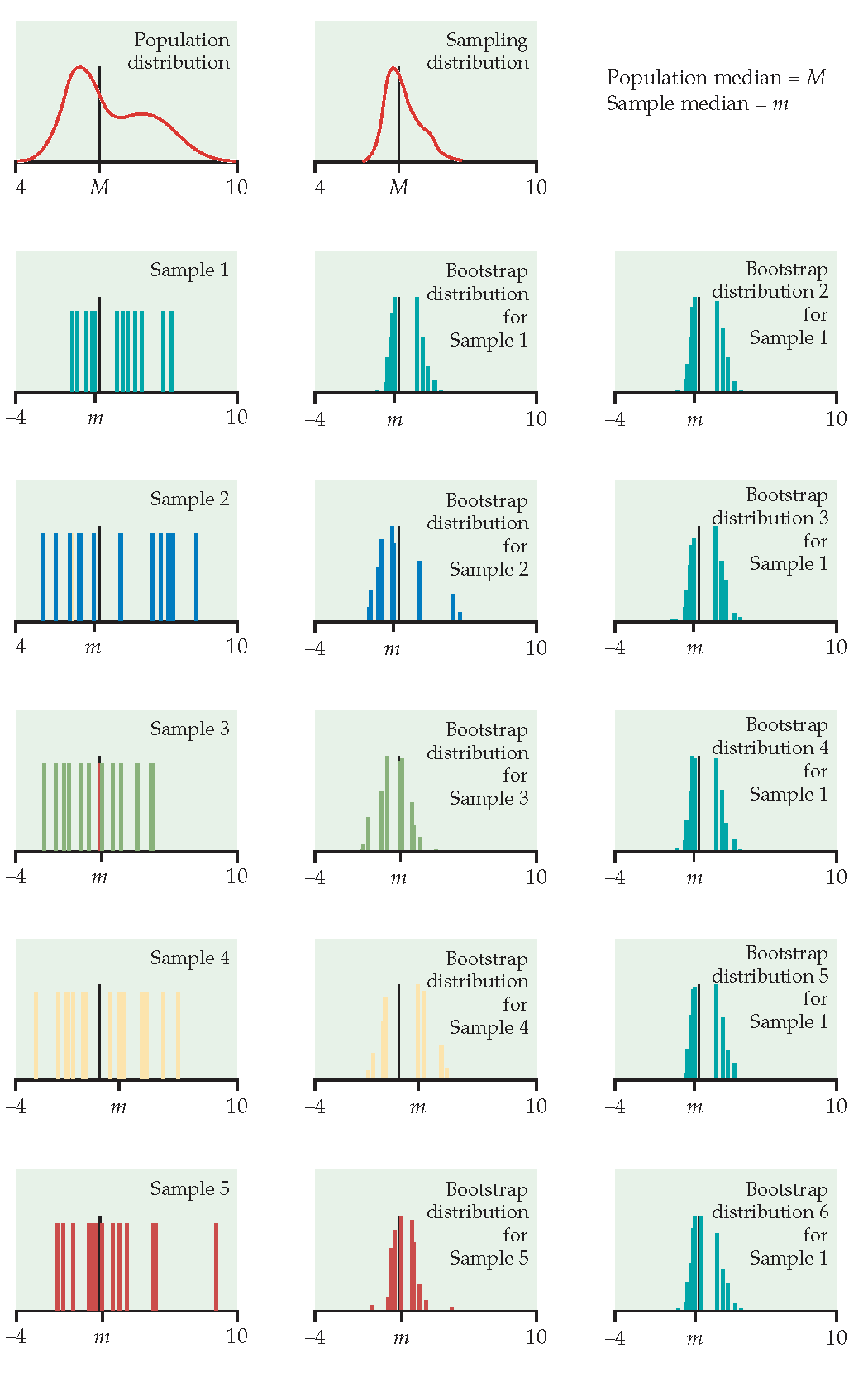
Just like repeatedly taking samples from the population, taking resamples from the sample allows us to characterize the bootstrap distribution which approximates the sampling distribution.

The bootstrap distribution approximates the shape, spread, & bias of the true sampling distribution.

From Hesterberg et al., Chapter 16 of Introduction to the Practice of Statistics by Moore, McCabe, and Craig. The left image represents the mean with n=50. The center image represents the mean with n=9. The right image represents the median with n=15.

Example

Everitt and Rabe-Hesketh (2006) report on a study by Caplehorn and Bell (1991) that investigated the time (days) spent in a clinic for methadone maintenance treatment for people addicted to heroin.
The data include the amount of time that the subjects stayed in the facility until treatment was terminated.
For about 37% of the subjects, the study ended while they were still the in clinic (status=0).
Their survival time has been truncated. For this reason we might not want to estimate the mean survival time, but rather some other measure of typical survival time. Below we explore using the median as well as the 25% trimmed mean. (From Chance and Rossman (2018), Investigation 4.5.3)

The data

# A tibble: 238 × 5
      id clinic status times  dose
   <dbl>  <dbl>  <dbl> <dbl> <dbl>
 1     1      1      1   428    50
 2     2      1      1   275    55
 3     3      1      1   262    55
 4     4      1      1   183    30
 5     5      1      1   259    65
 6     6      1      1   714    55
 7     7      1      1   438    65
 8     8      1      0   796    60
 9     9      1      1   892    50
10    10      1      1   393    65
# ℹ 228 more rows

Observed Test Statistic(s)

heroin |>
  summarize(obs_med = median(times), 
            obs_tr_mean = mean(times, trim = 0.25))

# A tibble: 1 × 2
  obs_med obs_tr_mean
    <dbl>       <dbl>
1    368.        378.

Bootstrapped data!

set.seed(4747)

heroin |> 
  sample_frac(size=1, replace=TRUE) |>
  summarize(boot_med = median(times), 
            boot_tr_mean = mean(times, trim = 0.25))

# A tibble: 1 × 2
  boot_med boot_tr_mean
     <dbl>        <dbl>
1      368         372.

Bootstrapping with `map()`.

n_rep1 <- 100
n_rep2 <- 20
set.seed(4747)

heroin

# A tibble: 238 × 6
      id clinic status times prison  dose
   <dbl>  <dbl>  <dbl> <dbl>  <dbl> <dbl>
 1     1      1      1   428      0    50
 2     2      1      1   275      1    55
 3     3      1      1   262      0    55
 4     4      1      1   183      0    30
 5     5      1      1   259      1    65
 6     6      1      1   714      0    55
 7     7      1      1   438      1    65
 8     8      1      0   796      1    60
 9     9      1      1   892      0    50
10    10      1      1   393      1    65
# ℹ 228 more rows

boot_stat_func <- function(df){ 
    df |> 
    mutate(obs_med = median(times),
           obs_tr_mean = mean(times, trim = 0.25)) |>
    sample_frac(size=1, replace=TRUE) |>
    summarize(boot_med = median(times), 
              boot_tr_mean = mean(times, trim = 0.25),
              obs_med = mean(obs_med),
              obs_tr_mean = mean(obs_tr_mean))}

boot_1_func <- function(df){
  df |> 
    sample_frac(size=1, replace=TRUE)
}

map(1:n_rep1, ~boot_stat_func(df = heroin)) |> 
  list_rbind()

# A tibble: 100 × 4
   boot_med boot_tr_mean obs_med obs_tr_mean
      <dbl>        <dbl>   <dbl>       <dbl>
 1     368          372.    368.        378.
 2     358          363.    368.        378.
 3     431          421.    368.        378.
 4     332.         350.    368.        378.
 5     310.         331.    368.        378.
 6     376          382.    368.        378.
 7     366          365.    368.        378.
 8     378.         382.    368.        378.
 9     394          386.    368.        378.
10     392.         402.    368.        378.
# ℹ 90 more rows

Data distributions

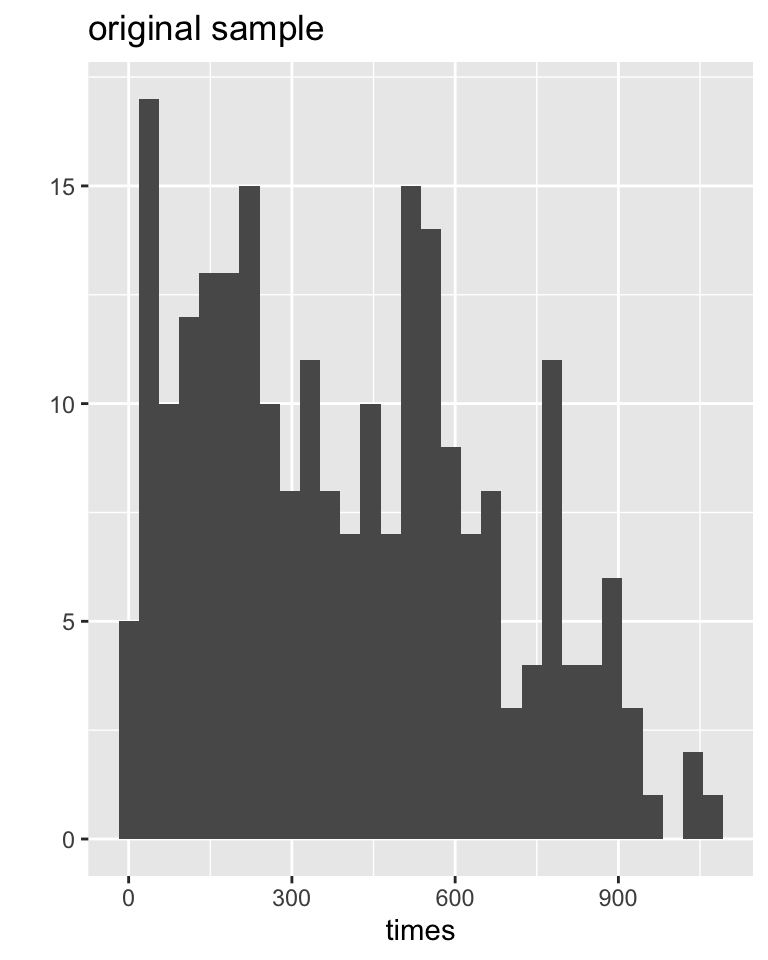
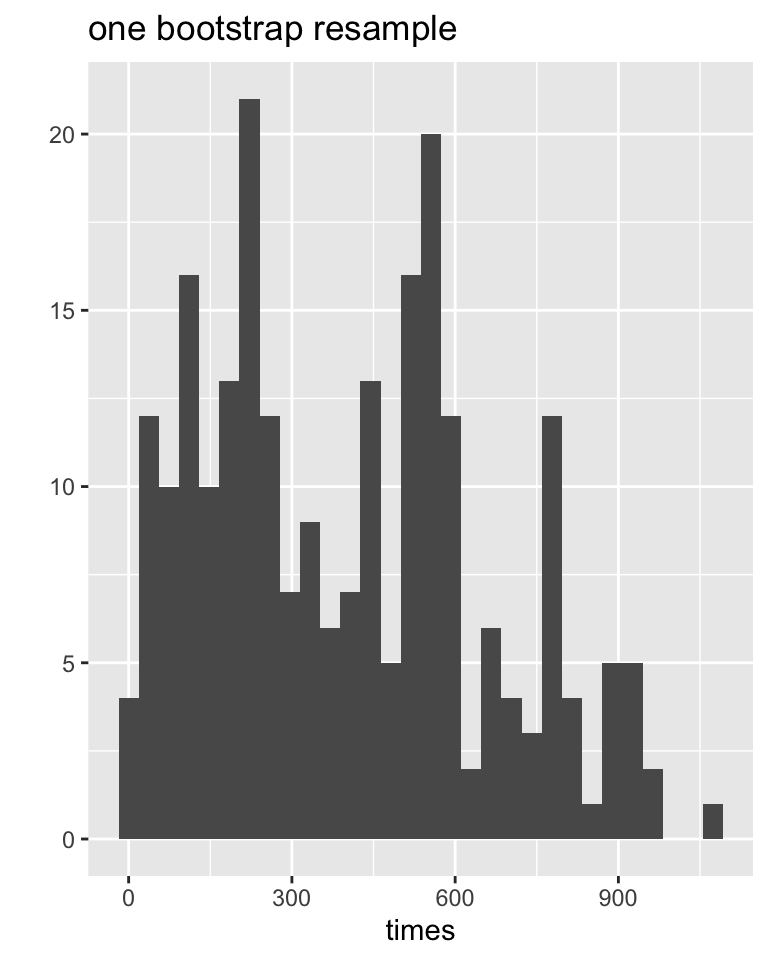
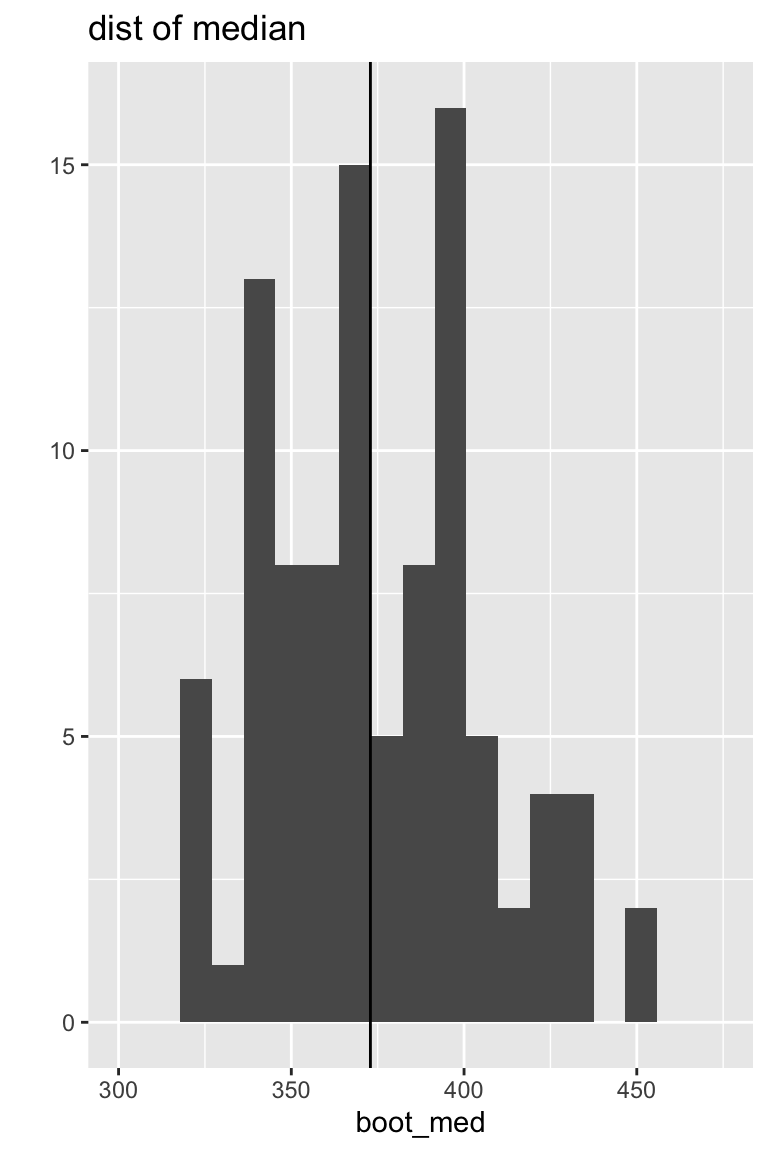
Sampling distributions

Both the median and the trimmed mean are reasonably symmetric and bell-shaped.

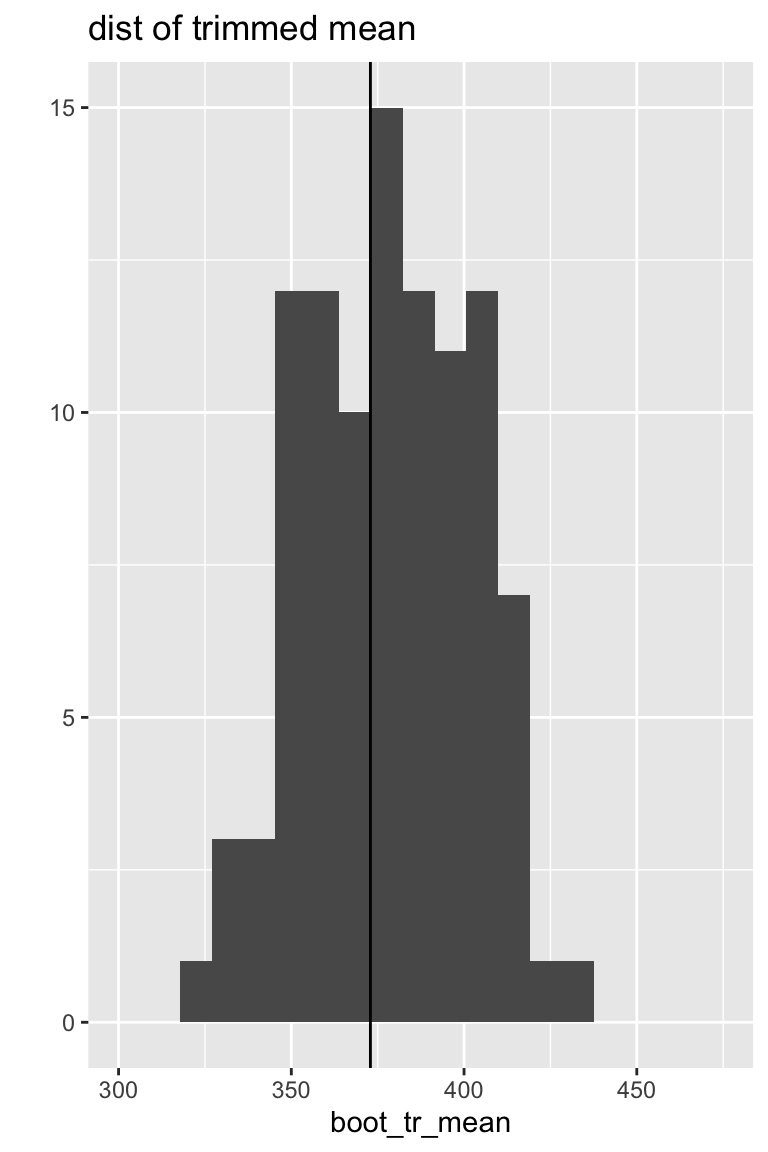
Agenda 10/16/24

Logic of CI
Normal CI using BS SE
Bootstrap-t (studentized) CIs
Percentile CIs
properties / advantages / disadvantages

Technical derivations

See in class notes on bootstrapping for the technical details on how to create different bootstrap intervals.

Bootstrapping with `map`

n_rep1 <- 100
set.seed(4747)

boot_stat_func <- function(df){ 
    df |> 
    mutate(obs_med = median(times),
           obs_tr_mean = mean(times, trim = 0.25)) |>
    sample_frac(size=1, replace=TRUE) |>
    summarize(boot_med = median(times), 
              boot_tr_mean = mean(times, trim = 0.25),
              obs_med = mean(obs_med),
              obs_tr_mean = mean(obs_tr_mean))}

boot_stats <- map(1:n_rep1, ~boot_stat_func(df = heroin)) |> 
  list_rbind()

boot_stats

# A tibble: 100 × 4
   boot_med boot_tr_mean obs_med obs_tr_mean
      <dbl>        <dbl>   <dbl>       <dbl>
 1     368          372.    368.        378.
 2     358          363.    368.        378.
 3     431          421.    368.        378.
 4     332.         350.    368.        378.
 5     310.         331.    368.        378.
 6     376          382.    368.        378.
 7     366          365.    368.        378.
 8     378.         382.    368.        378.
 9     394          386.    368.        378.
10     392.         402.    368.        378.
# ℹ 90 more rows

95% normal CI with BS SE

boot_stats |>
  summarize(
    low_med = mean(obs_med) + qnorm(0.025) * sd(boot_med),
    up_med = mean(obs_med) + qnorm(0.975) * sd(boot_med),
    low_tr_mean = mean(obs_tr_mean) + qnorm(0.025) * sd(boot_tr_mean),
    up_tr_mean = mean(obs_tr_mean) + qnorm(0.975) * sd(boot_tr_mean))

# A tibble: 1 × 4
  low_med up_med low_tr_mean up_tr_mean
    <dbl>  <dbl>       <dbl>      <dbl>
1    310.   425.        337.       420.

95% Percentile CI

boot_stats |>
  summarize(perc_CI_med = quantile(boot_med, c(0.025, 0.975)), 
            perc_CI_tr_mean = quantile(boot_tr_mean, c(0.025, 0.975)), 
            q = c(0.025, 0.975))

# A tibble: 2 × 3
  perc_CI_med perc_CI_tr_mean     q
        <dbl>           <dbl> <dbl>
1        321             335. 0.025
2        435.            420. 0.975

Double bootstrapping with `map`

n_rep1 <- 100
n_rep2 <- 20
set.seed(4747)

boot_stat_func <- function(df){ 
    df |> 
    mutate(obs_med = median(times),
           obs_tr_mean = mean(times, trim = 0.25)) |>
    sample_frac(size=1, replace=TRUE) |>
    summarize(boot_med = median(times), 
              boot_tr_mean = mean(times, trim = 0.25),
              obs_med = mean(obs_med),
              obs_tr_mean = mean(obs_tr_mean))}

boot_1_func <- function(df){
  df |> 
    sample_frac(size=1, replace=TRUE)
}

boot_2_func <- function(df, reps){
  resample2 <- 1:reps
  df |>
    summarize(boot_med = median(times), boot_tr_mean = mean(times, trim = 0.25)) |>
    cbind(resample2, map(resample2, ~df |> 
            sample_frac(size=1, replace=TRUE) |>
            summarize(boot_2_med = median(times), 
                       boot_2_tr_mean = mean(times, trim = 0.25))) |>
                list_rbind()) |> 
    select(resample2, everything())
}

boot_2_stats <- data.frame(resample1 = 1:n_rep1) |>
  mutate(first_boot = map(1:n_rep1, ~boot_1_func(df = heroin))) |>
  mutate(second_boot = map(first_boot, boot_2_func, reps = n_rep2))

Summarizing the double bootstrap

boot_2_stats |>
  unnest(second_boot) |>
  unnest(first_boot)

# A tibble: 476,000 × 12
   resample1    id clinic status times prison  dose resample2 boot_med
       <int> <dbl>  <dbl>  <dbl> <dbl>  <dbl> <dbl>     <int>    <dbl>
 1         1   257      1      1   204      0    50         1      368
 2         1   230      1      0    28      0    50         1      368
 3         1   229      1      1   216      0    50         1      368
 4         1   186      2      0   683      0   100         1      368
 5         1   119      2      0   684      0    65         1      368
 6         1    73      1      0   405      0    80         1      368
 7         1    41      1      1   550      1    60         1      368
 8         1    75      1      0   905      0    80         1      368
 9         1    68      1      0   439      0    80         1      368
10         1   224      1      1   546      1    50         1      368
# ℹ 475,990 more rows
# ℹ 3 more variables: boot_tr_mean <dbl>, boot_2_med <dbl>,
#   boot_2_tr_mean <dbl>

boot_2_stats |>
  unnest(second_boot) |>
  unnest(first_boot) |>
  filter(resample1 == 1)

# A tibble: 4 × 4
  skim_variable  numeric.mean numeric.sd numeric.p50
  <chr>                 <dbl>      <dbl>       <dbl>
1 boot_med               368         0          368 
2 boot_tr_mean           372.        0          372.
3 boot_2_med             365.       32.5        367.
4 boot_2_tr_mean         368.       21.5        367.

boot_t_stats <- boot_2_stats |>
  unnest(second_boot) |>
  unnest(first_boot) |>
  group_by(resample1) |>
  summarize(boot_sd_med = sd(boot_2_med),
            boot_sd_tr_mean = sd(boot_2_tr_mean),
            boot_med = mean(boot_med),  # doesn't do anything, just copies over
            boot_tr_mean = mean(boot_tr_mean))  |> # the variables into the output
  mutate(boot_t_med = (boot_med - mean(boot_med)) / boot_sd_med,
            boot_t_tr_mean = (boot_tr_mean - mean(boot_tr_mean)) / boot_sd_tr_mean)

  
boot_t_stats

# A tibble: 100 × 7
   resample1 boot_sd_med boot_sd_tr_mean boot_med boot_tr_mean boot_t_med
       <int>       <dbl>           <dbl>    <dbl>        <dbl>      <dbl>
 1         1        32.5            21.5     368          372.     -0.154
 2         2        24.2            18.8     358          363.     -0.619
 3         3        32.0            21.1     431          421.      1.81 
 4         4        49.1            34.0     332.         350.     -0.845
 5         5        22.7            13.4     310.         331.     -2.75 
 6         6        20.3            19.9     376          382.      0.148
 7         7        35.3            22.1     366          365.     -0.198
 8         8        15.0            16.4     378.         382.      0.367
 9         9        27.6            20.9     394          386.      0.761
10        10        38.5            19.6     392.         402.      0.481
# ℹ 90 more rows
# ℹ 1 more variable: boot_t_tr_mean <dbl>

95% Bootstrap-t CI

Note that the t-value is needed (which requires a different SE for each bootstrap sample).

boot_t_stats |>
  select(boot_t_med, boot_t_tr_mean)

# A tibble: 100 × 2
   boot_t_med boot_t_tr_mean
        <dbl>          <dbl>
 1     -0.154         -0.249
 2     -0.619         -0.790
 3      1.81           2.04 
 4     -0.845         -0.824
 5     -2.75          -3.50 
 6      0.148          0.235
 7     -0.198         -0.570
 8      0.367          0.261
 9      0.761          0.406
10      0.481          1.26 
# ℹ 90 more rows

boot_q <- boot_t_stats |>
  select(boot_t_med, boot_t_tr_mean) |>
  summarize(q_t_med = quantile(boot_t_med, c(0.025, 0.975)), 
            q_t_tr_mean = quantile(boot_t_tr_mean, c(0.025, 0.975)),
            q = c(0.025, 0.975))

boot_q

# A tibble: 2 × 3
  q_t_med q_t_tr_mean     q
    <dbl>       <dbl> <dbl>
1   -2.17       -2.20 0.025
2    1.78        2.06 0.975

boot_q_med <- boot_q |> select(q_t_med) |> pull()
boot_q_med

     2.5%     97.5% 
-2.170931  1.782708

boot_q_tr_mean <- boot_q |> select(q_t_tr_mean) |> pull()
boot_q_tr_mean

     2.5%     97.5% 
-2.204115  2.059893

boot_t_stats |>
  summarize(boot_t_CI_med = mean(boot_med) + boot_q_med*sd(boot_med),
            boot_t_CI_tr_mean = mean(boot_tr_mean) + boot_q_tr_mean * sd(boot_tr_mean),
            q = c(0.025, 0.975))

# A tibble: 2 × 3
  boot_t_CI_med boot_t_CI_tr_mean     q
          <dbl>             <dbl> <dbl>
1          309.              331. 0.025
2          425.              421. 0.975

Comparison of intervals

The first three columns correspond to the CIs for the true median of the survival times. The second three columns correspond to the CIs for the true trimmed mean of the survival times.

CI	Lower	Obs Med	Upper	Lower	Obs Tr Mean	Upper
Percentile	321	367.50	434.58	334.86	378.30	419.77
w BS SE	309.99	367.50	425.01	336.87	378.30	419.73
BS-t	309.30	367.50	425.31	331.03	378.30	421.17

(Can’t know what the Truth is…)

What makes a confidence interval procedure good?

That it captures the true parameter in \(1-\alpha \cdot\) 100% of the datasets.
That it produces narrow intervals.

What else about intervals?

CI	Symmetric	Range Resp	Trans Resp	Accuracy	Normal Samp Dist?	Other
Boot SE	Yes	No	No	1st order	Yes	Parametric assumptions, \(F(\hat{\theta})\)
Boot-t	No	No	No	2nd order	Yes/No	Computationally intensive
perc	No	Yes	Yes	1st order	No	Small \(n \rightarrow\) low accuracy
BCa	No	Yes	Yes	2nd order	No	Limited parametric assumptions

References

:::

References

Caplehorn, JR, and J Bell. 1991. “Methadone Dosage and Retention of Patients in Maintenance Treatment.” The Medical Journal of Australia 154 (3): 195–99.

Chance, Beth, and Allan Rossman. 2018. Investigating Statistics, Concepts, Applications, and Methods. 3rd ed. http://www.rossmanchance.com/iscam3/.

Everitt, Brian S., and Sophia Rabe-Hesketh. 2006. Handbook of Statistical Analyses Using Stata. Chapman & Hall.

Reuse

CC BY 4.0

Other Formats

Agenda 10/7/24

Why bootstrap?

Variability

Intuitive understanding

Basic Notation

Ideally

Bootstrap Procedure

Bootstrap Notation

What do we get?

Example

The data

Observed Test Statistic(s)

Bootstrapped data!

Bootstrapping with map().

Data distributions

Sampling distributions

Agenda 10/16/24

Technical derivations

Bootstrapping with map

95% normal CI with BS SE

95% Percentile CI

Double bootstrapping with map

Summarizing the double bootstrap

95% Bootstrap-t CI

Comparison of intervals

What makes a confidence interval procedure good?

What else about intervals?

References

References

Reuse

Bootstrapping with `map()`.

Bootstrapping with `map`

Double bootstrapping with `map`